Je vais vous donner mon astuce qui me permet de toujours bien formuler mes théorèmes. Dans cette article, je ne ferai pas la distinction entre théorèmes, propriétés, axiomes, lois, réciproques… Mon astuce marche pour toutes ces catégories. Je vais donc vous parler du théorème dans son sens général. Et vous verrez que cela ne s’applique pas qu’aux maths !

Principe du théorème.

Le principe est simple : on part d’un élément qu’on connaît pour en déduire un autre ensemble d’éléments.

Je sais quelque chose, j’en conclus autre chose.

Exemple :

“Les nombres paires sont divisibles par deux.”

(Je sais que c’est un nombre pair, j’en conclu automatiquement qu’il est divisible par 2.)

Je différencie plusieurs structures différentes de théorèmes :

Première structure : une seule donnée qui implique une conclusion.

C’est la structure la plus simple. J’ai une donnée, je peux conclure immédiatement une information. L’exemple donné précédemment est un très bon exemple :

“Les nombres pairs sont divisibles par deux.”

Mais également :

“Un triangle isocèle a deux côtés égaux.”

(Je sais que c’est un triangle isocèle, je vais donc pouvoir conclure de manière immédiate qu’il a deux côtés égaux.)

Et vous verrez que cela ne s’applique pas qu’aux maths. En réalité, dans notre cerveau nous avons énormément de petits théorèmes de ce genre qui permettent de lier une information à une autre information, du genre :

“Un rossignol est un oiseau.”

(Si on me dit que c’est un rossignol, mon cerveau conclut automatiquement que c’est un oiseau !)

On a également le fameux théorème de Pythagore qui est ainsi bâti. Je sais que je suis dans un triangle rectangle, je peux donc dire que le carré de l’hypoténuse est égale à la somme des carrés des deux autres côtés. Voici l’intitulé :

“Dans un triangle rectangle, le carré de l’hypoténuse est égale à la somme des carrés des deux autres côtés.”

L’hypothèse (donnée en vert) suivant les cas peut être séparé de la conclusion par les verbes être, avoir… parfois même un virgule suffit (théorème de Pythagore).

Avec le Si… Alors.

On pourra toujours structurer un théorème avec “Si… alors…”, mais cela n’est pas une obligation.

“Si un nombre est pair, alors il est divisible par deux.”

“Si un triangle est isocèle, alors il a deux côtés égaux.”

“Si c’est un rossignol, alors c’est un oiseau.”

“Si un triangle est rectangle, alors le carré de l’hypoténuse…”

Personnellement, je réserve la structure du si… alors… pour les réciproques (voir le prochain article).

Deuxième structure : deux données qui impliquent une conclusion.

Données de même niveau :

première information et deuxième information => conclusion.

Souvent => qu’on appelle “implication”, s’exprime par un verbe comme “donnent, forment, sont…”

“Deux droites parallèles et une droite sécante forment des angles alternes-internes égaux.”

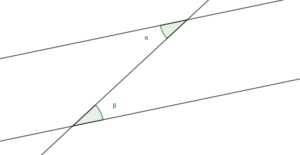
α = β

On peut également remplacer le “et” par simplement une “,” :

“Sur deux droites parallèles, une droite sécante forme des angles alternes-internes égaux.”

On retrouve toujours nos deux informations pour aboutir à la même conclusion.

Ces deux mêmes informations peuvent aussi être reliées par un verbe ou un adjectif à la place de “et” :

“Deux droites parallèles coupées par une sécante forment des angles alternes-internes égaux.”

Une donnée situe, l’autre donnée précise la première.

Pour lier ces deux données on utilise souvent “qui a”

première info qui a telle propriété => conclusion.

Ici => est plutôt exprimé par le verbe “être”.

“Un rectangle qui a deux côtés adjacents égaux est un carré.”

“Un triangle qui a deux côtés égaux est un triangle isocèle”

“Un oiseau qui a la gorge rouge est un rouge-gorge.”

Remarque : on peut souvent exprimer le théorème où les deux données sont de “même niveau” avec l’autre formulation, c’est à dire en considérant une donnée qui situe et l’autre qui précise :

“Deux droites parallèles qui sont coupées par une sécante forment des angles alternes-internes égaux.”

Avec le Si… alors :

“Si deux droites parallèles sont coupées par une sécante, alors elles forment des angles alternes-internes égaux.”

Clique ici si tu ne veux pas faire l’exercice et voir directement l’article suivant : comment est construite une réciproque ?

sinon…

À vous de jouer : formuler correctement ces théorèmes.

Avec une information :

Multiples de 4 => nombres pairs.

Avec deux informations :

Parallélogramme + diagonales perpendiculaires => losange.

Droites parallèles + sécante => angles correspondants égaux.

Triangle + deux angles égaux => triangle isocèle.

Clique ici pour connaître les réponses.